深度學習模擬密度泛函計算初試筆記（二）

一、前言

如深度學習模擬密度泛函計算初試筆記（一）所言，對於單水分子體系的優化而言，採取笛卡爾坐標進行輸入是一種不經濟的做法。採取內坐標的方式進行輸入會明顯更優。因此，筆者進一步嘗試一下能否通過內坐標輸入的方式對單水分子體系進行優化。

二、內坐標確定

內坐標是一種通過鍵長、鍵角、二面角對化學體系進行表示的方法，比起笛卡爾坐標而言，化學意義更加明顯，且坐標之間的耦合相較於笛卡爾坐標較弱，因此在Gaussian等量子化學程序的實際優化之中也更為常用（Gaussian默認的優化是在冗餘內坐標下進行的）。

慾通過內坐標表達一個水分子，需要兩個O-H鍵長與H-O-H鍵角共計三個內坐標。然而參考數據集中是以笛卡爾坐標進行表示的，因此需要將其轉化為內坐標。轉化後，每個數據集的X依次為r1、r2、a1，y仍為單點能，其數據集示例如下（可於文末下載）：

X[0] = [1.8934187377789702, 1.8770720543831665, 41.564869986605515]
y[0] = -76.1141702491

X[1] = [1.668518356982647, 2.502124716523313, 143.2600654969497]
y[1] = -76.0434955957

…………

X[1499] = [1.7872336934039146, 2.627109619214445, 149.41043492598493]
y[1499] = -76.0138053880

三、訓練集與測試集的構建

筆者採取了和上文相同的訓練集與測試集的構建方法：

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, random_state=24)

得到訓練集1125個數據點，測試集375個數據點。

四、深度學習訓練

筆者採取tanh作為激活函數，隱藏層設置為[20, 20]，正則化參數alpha設置為0.0001：

from sklearn.neural_network import MLPRegressor

mlp = MLPRegressor(activation="tanh", hidden_layer_sizes=[20, 20], alpha=0.0001, solver='lbfgs', max_iter=10000, random_state=45)
mlp.fit(X_train, y_train)

僅僅0.7秒便完成了訓練，模型表現為：

mlp.score(X_train, y_train)
0.9919439484627582

mlp.score(X_test, y_test)
0.9724540032809257

可以看到模型的表現非常好，接下來測試一下該模型對水分子結構優化的性能。

五、利用深度學習對水分子進行結構優化

由於CMA-ES方法在各優化變量的數值範圍接近時表現良好，因此需要對優化數值進行放縮（對於此前笛卡爾坐標的優化，由於各優化變量的數值範圍接近，故無需放縮）。筆者採取的是將鍵角數據除以100的方式，因此能量函數為：

def energy(xyz):
    return mlp.predict(scaler.transform([[xyz[0], xyz[1], xyz[2]*100]]))[0]

優化代碼為：

import cma

init_xyz = [1.0, 1.0, 1.2]

es = cma.CMAEvolutionStrategy(init_xyz, 0.2)
es.optimize(energy)

優化僅耗時0.2秒，其結果為：

es.result.xbest
array([0.95409839, 0.97375311, 1.05703081])

DFT優化得到的參考數據為：

r1 = 0.9687425816144349
r2 = 0.968745685706006
a1 = 103.65158225677882

對比如下：

	r1	r2	a1
深度學習	0.9541	0.9738	105.70
DFT	0.9687	0.9687	103.65
相對偏差	-1.5%	+0.5%	+2.0%

結果對比

可以看到，無論是鍵長還是鍵角，深度學習模型都給出了非常好的優化結果，誤差在2.0%以內。足以見得以內坐標方式構建的深度學習模型的強大之處。

六、柔性掃描嘗試

柔性掃描即以一定步長掃描分子的某一（些）坐標，對其它坐標進行優化的一種限制性優化方法。內坐標的一個優勢是可以方便地進行柔性掃描。筆者嘗試使用深度學習模型進行柔性掃描，掃描內容為H-O-H鍵角，從80°開始，每5°掃描一次，直到130°為止。

angle = 80

def energy(xyz):
    return mlp.predict(scaler.transform([[xyz[0], xyz[1], angle]]))[0]

import cma

for angle in range(80, 135, 5):
    init_xyz = [0.96, 0.96]
    es = cma.CMAEvolutionStrategy(init_xyz, 0.2, {"seed":74})
    es.optimize(energy)
    print("angle = "+str(angle)+", r = "+str(es.result.xbest)+", E = "+str(es.result.fbest))

結果如下：

a1	r1	r2	E
80	0.9656	1.0488	-76.3888
85	0.9628	1.0333	-76.3954
90	0.9605	1.0180	-76.4004
95	0.9586	1.0032	-76.4040
100	0.9566	0.9889	-76.4062
105	0.9544	0.9756	-76.4070
110	0.9518	0.9633	-76.4066
115	0.9487	0.9525	-76.4050
120	0.9450	0.9435	-76.4024
125	0.9406	0.9363	-76.3989
130	0.9359	0.9313	-76.3945

掃描結果

以B3LYP/6-31G*進行同樣的柔性掃描，得到參考數據進行對比，作圖如下：

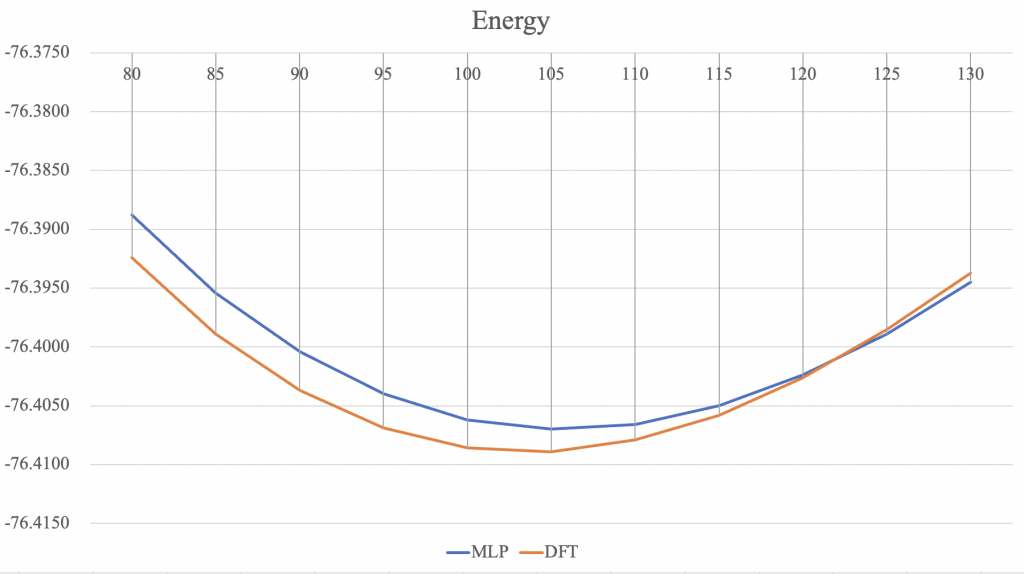
可見能量曲線走勢正確，最低值接近，且低鍵角部分深度學習模型與DFT計算的能量差近乎恆定值（由於能量只有相對值才有意義，故對低鍵角部分的能量擬合可以認為定量正確）。對於高鍵角部分，能量擬合定性正確，定量上存在誤差可能源自訓練集不夠完備。

鍵長部分的結果較為有趣，其中r1與DFT計算的鍵長保持近乎恆定的差值，而r2變動幅度則較大，整體鍵長變化為定性正確。值得注意的是，本模型訓練過程中是未利用對稱性的，即未人為指定r1、r2相等（對應地，DFT計算時也加入了nosymm關鍵字以避免額外對稱性的影響）。在此後的工作中，可以考慮引入對稱性進行計算，以提高模型的精確度，使其更加符合客觀現實。

七、討論

內坐標比起笛卡爾坐標的優勢有二。首先，內坐標具備更明確、更直觀的化學意義。例如單水分子的體系，其三個內坐標分別對應鍵長或鍵角，直指化學問題的本質。其次，內坐標彼此之間耦合較低，且對分子整體的平移、旋轉不敏感。這些優點使得Gaussian等量化軟件多以與內坐標類似的冗餘內坐標作為優化的默認方式。然而，內坐標同樣也是具備缺點的：內坐標的構建較為困難，特別是對較大的體系而言。當體系變大時，涉及的內坐標數量也會隨之升高（而且往往是非線性升高），如何構建科學、簡潔的內坐標，便成為了一個問題。對於較大的體系，構建得不夠理想的內坐標經常會存在嚴重的耦合，有時需要藉助虛擬原子等方式進行內坐標的構建。同時，內坐標的構建具備一定的隨意性，對於一個體系而言時常有多種內坐標的構建方式，從而導致內坐標的構建較為困難。同時，內坐標還存在不易作圖等問題，因此使得內坐標還暫時無法取代笛卡爾坐標。

對於較小的體系，內坐標可較為簡單地手動構造；而對於較大的體系，內坐標的構建往往依賴於自動化的方法構建。筆者當前使用的單水分子體系是一個非常小的體系，因此內坐標具備充分的優勢。對於較大的體系，內坐標是否依然適用呢？筆者今後有時間時會進一步研究討論。

八、參考數據集下載

ref2.txt 下载

Weida

2022年8月21日