一、前言
演化策略(Evolutionary Strategy)是最古老的演化算法之一,其实现非常容易,且参数简单、易于调控,可用于许多优化问题的解决。其中,(1+1)演化策略又是演化策略中最简单的一种。笔者近期正在学习演化算法,因此将本文作为一个练习的记录。
二、(1+1)演化策略介绍
(1+1)演化策略是一种只包含一个个体,且只使用变异操作的一种演化算法。其思想可概括如下:给定一个初始态,计算损失函数(Loss Function,用于评估模型的指标)。随后随机在初始态周围较近的地方选取一个新点,计算损失函数。如果新点的损失函数较小(意味着新点所代表的模型更好),则将新点作为初始态;如果新点的损失函数较大,则重新选择一个新点。如此循环,直到达到既定目标(即收敛,表现为损失函数低于一给定的值)或达到最大循环次数停止。可见,(1+1)演化策略本质上是一种贪心算法(Greedy Algorithm),即总是选取当下最优的情况的算法。
三、多项式函数拟合尝试
下面用Python语言结合(1+1)演化策略进行一个多项式函数拟合的尝试。目标函数设为y = 9x^3 + 8x^2 + 2x + 4。首先构建计算函数与损失函数:
def cal(p, x): #p为多项式系数
result = 0
for i in range(len(p)):
result += p[i] * (x ** i)
return result
def cal_loss(p, x, y): #p为多项式系数,使用RMSE作为损失函数
loss = 0
for i in range(len(x)):
loss += (cal(p, x[i]) - y[i]) ** 2
loss = (loss / len(x)) ** 0.5
return loss随后给定参考值,这里选择了x = 1, 2, 3, 4时的值:
x = [1, 2, 3, 4]
y = [23, 112, 325, 716]
演化策略代码如下:
import random
p = [0,0,0,0] #初始值,设为各项均为0
p_n = p.copy()
loss = cal_loss(p, x, y)
dev = 1 #初始偏移量,这里先设为1
max_times = 10 ** 7 #不设收敛标准,统一优化10,000,000步
for times in range(max_times):
for i in range(len(p)):
p_n[i] = p[i] + random.uniform(-dev, dev)
loss_n = cal_loss(p_n, x, y)
if loss_n < loss:
loss = loss_n
for i in range(len(p)):
p[i] = p_n[i]
if (times != 0 and times % 10000 == 0):
dev = 1 #偏移量更新,这里先不进行更新
print(str(times) + " " + str(loss)) #每10,000步输出一次损失函数最后输出优化结果:
p.reverse() #调整p的项目顺序使其更接近多项式阅读习惯
print(str(max_times) + " times finished!")
print(p)
print("RMSE = " + str(loss))运行后,得到结果(由于随机种子问题,多次运行得到的结果可能不同):
[9.006540223303382, 7.934732900551717, 2.1888675522686447, 3.842802581599673]
RMSE = 0.020157539926575947可以看到,算法给出了拟合结果:y = 9.01x^3 + 7.93x^2 + 2.19x + 3.84。这个结果谈不上好,根据优化过程分析,得出其损失函数图如下:
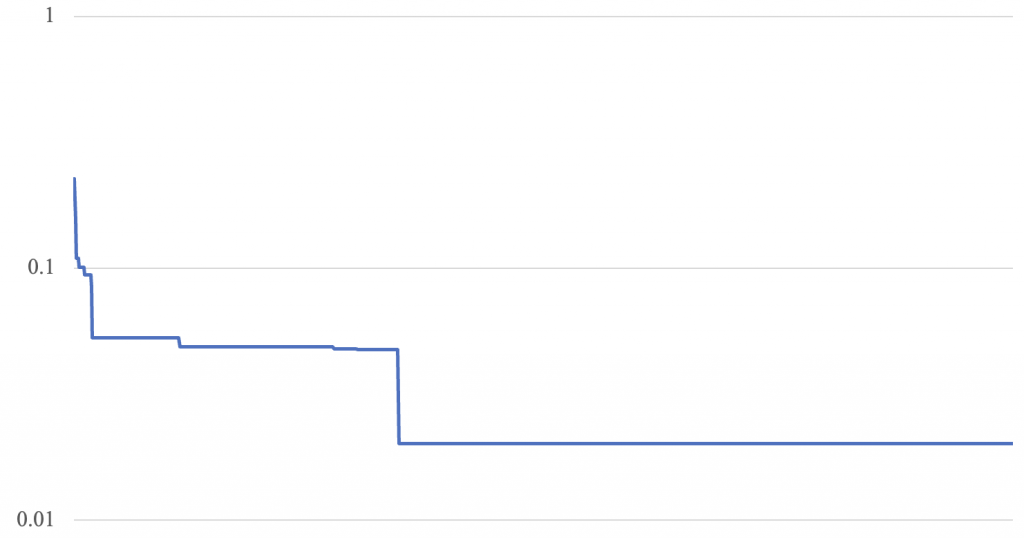
究其原因,恒定的偏移量(即dev,这里直接设置成了1)对于这个问题的求解过大了。例如最终给出的值,其最大的系数误差仅为0.19(为第三项为2.19,真实值为2.00),意味着每次是在1.19-3.19之前去随机选择一个值,比起2.19更接近2.00的概率并不高(仅19%),更不用说其中误差较低的值了(例如第一项的9.01,真正值为9.00,意味着只有1%的概率选择到误差更小的值)。同时,每次“变异”是四项同步进行的,意味着即使某项“碰巧”更接近真实值,也可能被其它误差变大的项影响,使得损失函数并未变小。事实上,多项式次数越低的值越容易受此影响,不易收敛。
为克服这些问题,笔者尝试采取了更小的偏移量,当偏移量恒为0.01时,结果如下:
[8.999734623524132, 8.001920166308894, 1.995836470501292, 4.002674364962314]
RMSE = 0.00021488395475822926拟合结果已大幅好转,损失函数图像如下:
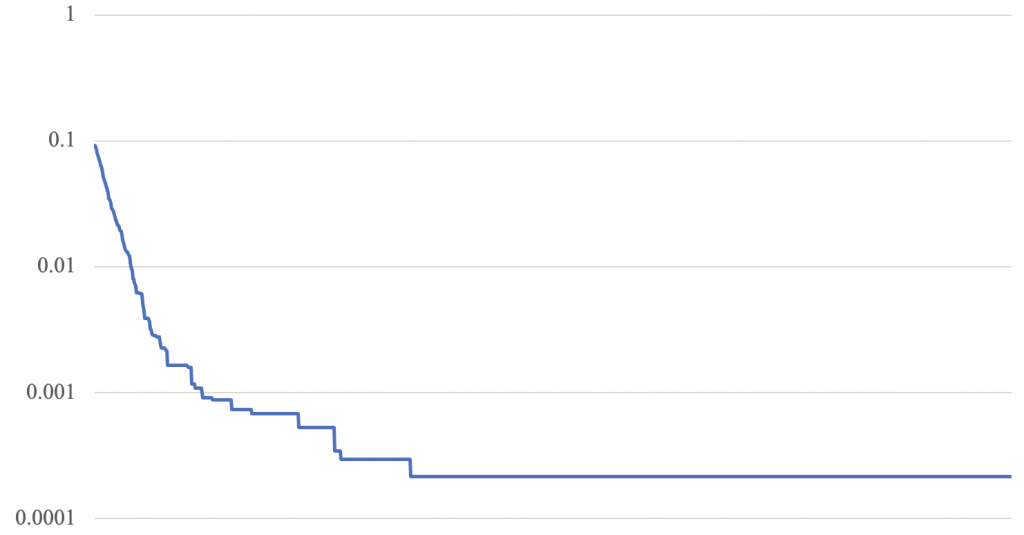
可以发现损失函数下降是呈阶梯状的,这其实意味着和dev=1时同样的问题,即后期误差较小时,偏移量偏高导致进一步收敛的概率降低。虽然dev=0.01本身很小,但对于后期误差较小的情况则依然显得比较大。但进一步降低dev可能会导致开始时收敛太慢。因此,能否不使用恒定的dev,改为动态的dev使得收敛更加科学呢?很容易想到的一个方式是随着步数调整dev。首先尝试dev = 100 / steps(初始仍为1)。本文中所有调整dev都是每10,000步调整一次,结果如下:
[8.999999736464373, 8.000002196461649, 1.9999944659778188, 4.000003909897465]
RMSE = 2.874331197238151e-07可以看到随步数调整dev果然得到了很好的结果,RMSE仅为10^(-7)数量级。损失函数图像如下:
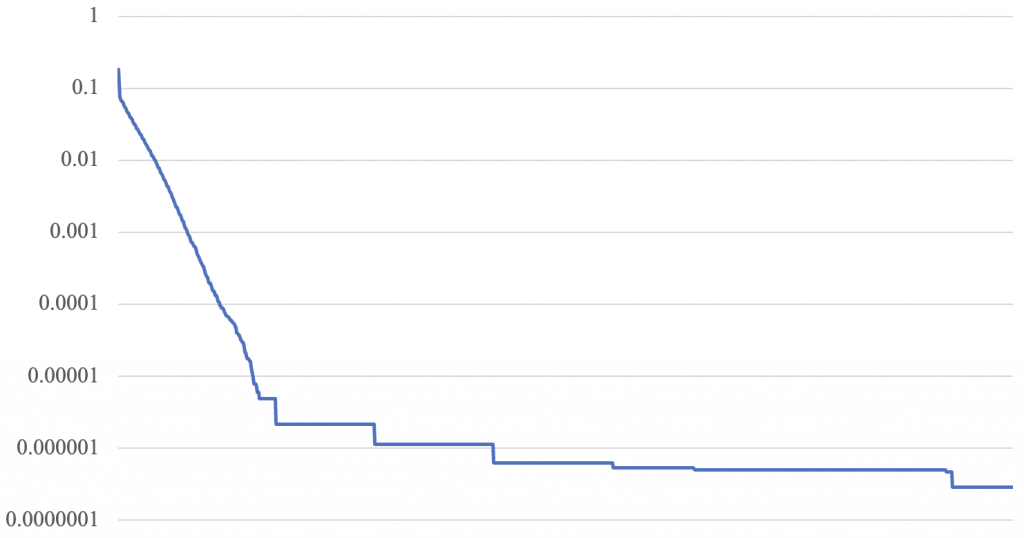
演化策略是有一定随机性的,正如自然界的变异也是随机的一样。依照步数调整dev的一个问题是,步数并不一定能够很好地反映误差。步数是固定的,误差是随机的,以一个固定的参数去拟合随机的参数,必然存在拟合误差的问题。因此,能否根据训练进度本身去调整dev呢?很容易想到的一点是根据损失函数(即RMSE)的值去调整dev。尝试dev = RMSE(初始仍为1),结果如下:
[9.000000000000105, 7.999999999999229, 2.0000000000016827, 3.9999999999989684]
RMSE = 5.1728291973635394e-14于是我们得到了一个极其理想的结果,RMSE仅为10^(-14)数量级,比起之前的10^(-7)数量级仍然有极大的提升。损失函数图像如下:
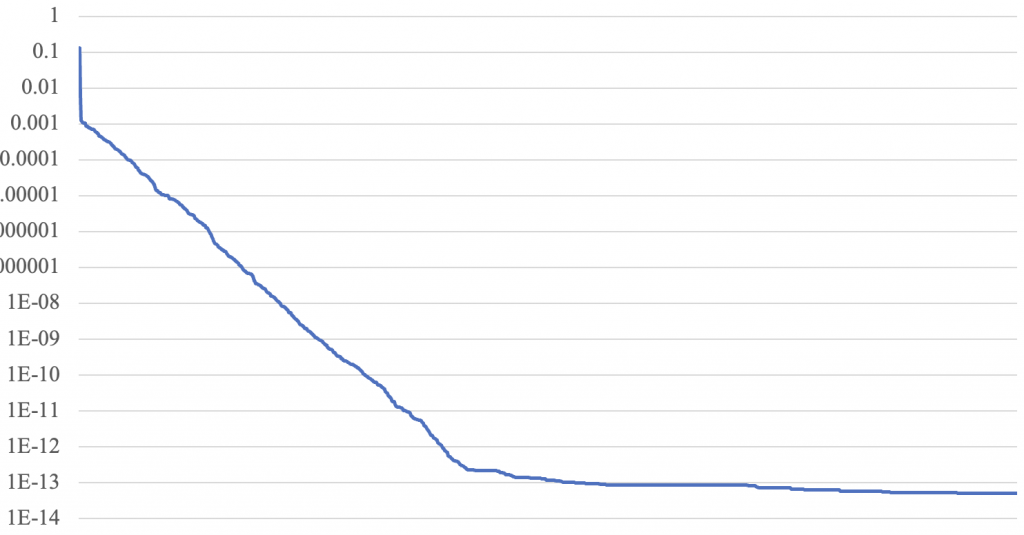
可见损失函数维持了相当长时间的稳定下降,也足以说明随优化进度动态调整dev的科学性。通过观察损失函数图像,发现训练过程接近一半时,损失函数下降速度变慢,逐渐收敛,单独取出训练的后半段损失函数图像,查看如下(此图非对数坐标):
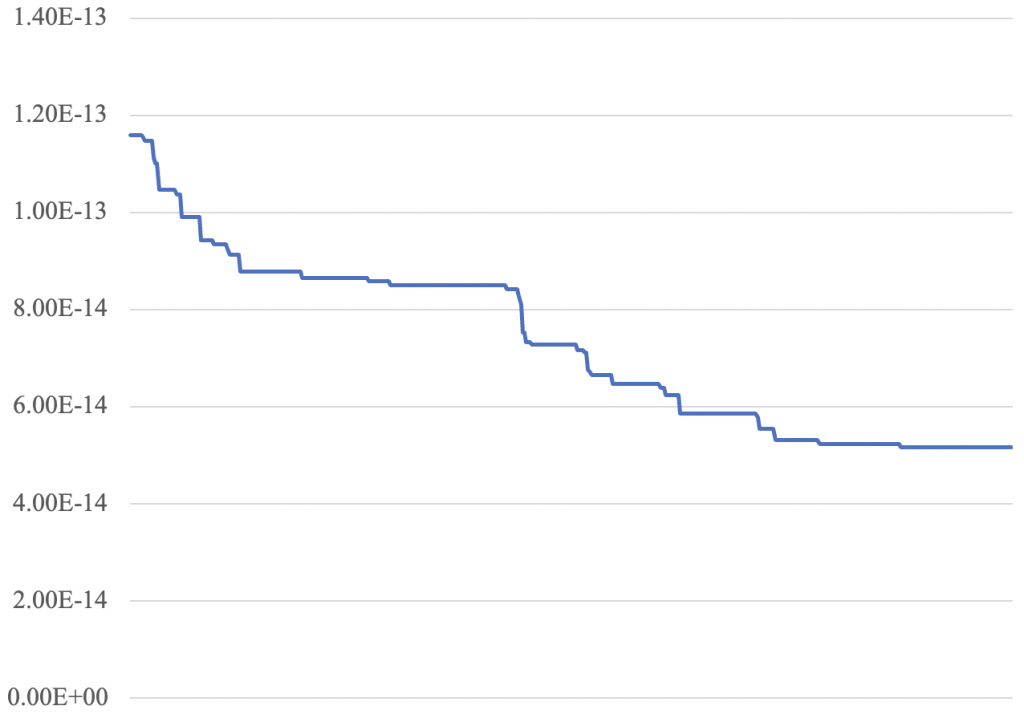
可见损失函数在后半段呈现阶梯状缓慢下降的趋势。若仍要追求更高精度,则可尝试构建更加复杂的dev函数,由于篇幅所限,本文就不再进行展开了。
四、总结
事实上,以上仅仅是对于dev一项的调整,对应的是机器学习中的“学习率”(Learning Rate),这也是(1+1)演化策略中最关键的超参数(Hyperparameter)。(1+1)演化策略只是最基本的演化策略,其效率不高,且易于收敛到局部最优解(因为其本质上是一种贪心算法)。针对它的问题,使用者可以进行各种各样的改进。例如,每次可生成超过一个子本、对每个参数可进行分别变异、可引入“杂交”策略、可记录多层父本的信息综合利用等等。本文只是介绍一下最基本的内容,具体种种,还需要不断在实际问题中探索发现。笔者本身并非计算机专业,因此可能有些地方写得不够准确,还望读者不吝赐教!
